Solution
Step 1:
The function reaches a maximum where the derivative is equal to 0.
Find the first derivative of the function.
Step 2:
Write the function

Step 3
Find the first derivative
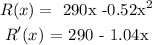
Step 4:
The function reaches a maximum where the derivative is equal to 0.
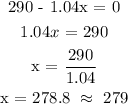
So the number of units which produce the maximum revenue = 279
Step 5:
Substituting this value in the original equation gives the revenue:
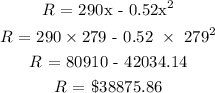
Maximum revenue = $38875.86