Question

in a recent survey, 60% of the community favored building a health center in their neighborhood. If 14 citizens are chosen, find the probability that exactly 11 of them favor the building of the health center. Round to the nearest thousandth.

Answer 1

0.085

Step-by-step explanation:

To find the probability, we will use the binomial distribution because there are n identical events ( 14 citizens), with a probability of success (p = 60%). Then, the probability can be calculated as:

`P(x)=\text{nCx}\cdot p^x\cdot(1-p)^(n-x)`

Where nCx is equal to

`\text{nCx}=(n!)/(x!(n-x)!)`

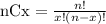
So, to find the probability that exactly 11 of them favor the building of the health center, we need to replace x = 11, n = 14, and p = 0.6

`14C11=(14!)/(11!(14-11)!)=(14!)/(11!(3!))=364`
`\begin{gathered} P(11)=364(0.6)^(11)(1-0.6)^(14-11) \\ P(11)=0.085 \end{gathered}`

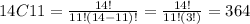
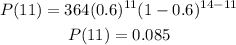
Therefore, the probability that exactly 11 of them favor the building of the health center is 0.085