The formula for compounding continuously is :
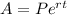
where A is the future amount
P is the principal amount
e is a constant
r is the rate of interest
and
t is the time in years.
The question stated that the investment will be doubled, so the future amount will be twice the principal amount.
A = 2P
The rate of interest is 3.7%
e is a constant approximately equal to 2.71828..
Subsitute the values to the formula and solve the value of t :
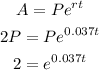
Take the natural logarithm of both sides,
note that ln e = 1
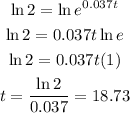
The answer is 18.73 years