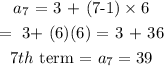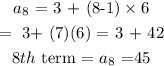![\operatorname{Re}cursive\colon a_n=a_(n-1)+6]()
see explanation below
Step-by-step explanation:
8) 3, 9, 15, 21, 27
The common difference = 15-9 = 9-3
The common difference = d = 6
Hence, it is an arithmetric sequence
The recursive formula:
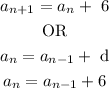
The appropriate formula:

The next three numbers in the sequence: