Step-by-step explanation
Given that the area of the rectangular certificate is 35 inches and its perimeter is 24 inches. Therefore, if L represents the length of the certificate and w represents its width, therefore;
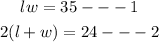
Therefore, we can say
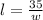
We will substitute the above in equation 2

Since the width must be shorter than the length therefore the width will be 5 inches.
Hence;

Answers:
The dimensions are:
Length = 7 inches
Width = 5 inches