Question

A rectangular certificate has an area of 35 square inches. Its perimeter is 24 inches. What arethe dimensions of the certificate?

Answer 1

Step-by-step explanation

Given that the area of the rectangular certificate is 35 inches and its perimeter is 24 inches. Therefore, if L represents the length of the certificate and w represents its width, therefore;

`\begin{gathered} lw=35---1 \\ 2(l+w)=24---2 \end{gathered}`

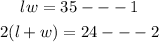
Therefore, we can say

`l=(35)/(w)`

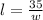
We will substitute the above in equation 2

`\begin{gathered} 2((35)/(w)+w)=24 \\ (70)/(w)+2w=24 \\ multiply\text{ though by w} \\ 70+2w^2=24w \\ 2w^2-24w+70=0 \\ 2(w^2-12w+35)=0 \\ w^2-7w-5w+35=0 \\ (w-7)-5(w-7)=0 \\ (w-7)(w-5)=0 \\ w=7\text{ or w=5} \end{gathered}`

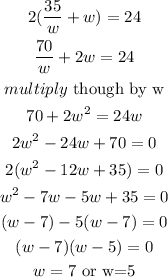
Since the width must be shorter than the length therefore the width will be 5 inches.

Hence;

`l=(35)/(5)=7`

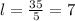
Answers:

The dimensions are:

Length = 7 inches

Width = 5 inches