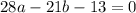Question

Find the equation of the normal in the form ax + by + c = 0 at the point where x = 4, for thecurve8=y = 2x2 - 4x3 - - 1х

Answer 1

We are given the equation of a curve;

`2x^2-4x^{(3)/(2)}-(8)/(x)-1`

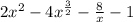
To solve this we begin by taking the derivative of this curve. Note that the slope of this curve is its first derivative.

We now have;

`\begin{gathered} (d)/(dx)(2x^2-4x^{(3)/(2)}-(8)/(x)-1 \\ =4x-6x^{(1)/(2)}-(8)/(x^2) \end{gathered}`

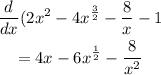
At this point we should note that the slope (gradient) is the value of this first derivative when x = 4.

We can now plug in this value and we'll have;

`\begin{gathered} f^(\prime)(x)=4x-6x^{(1)/(2)}-(8)/(x^2) \\ At\text{ } \\ x=4,\text{ we would have;} \\ f^(\prime)(4)=4(4)-6(4)^{(1)/(2)}-(8)/(4^2) \\ f^(\prime)(4)=16-6(2)-(8)/(16) \\ f^(\prime)(4)=16-12-(1)/(2) \\ f^(\prime)(4)=3(1)/(2) \\ OR \\ f^(\prime)(4)=(7)/(2) \end{gathered}`

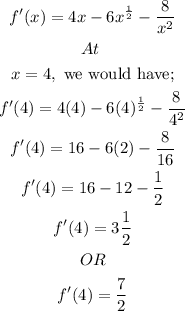
Now we can see the slope of the curve. The slope of the normal line perpendicular to the tangent of the curve is a negative inverse of this.

The negative inverse of 7/2 would be;

`\begin{gathered} \text{Gradient}=(7)/(2) \\ \text{Gradient of perpendicular}=-(2)/(7) \end{gathered}`

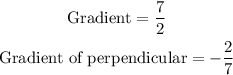
Now to use this value to derive the equation in the form

`ax+by+c=0`

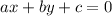
We start by expresing this in the form;

`y=mx+b`

We now have;

`y=-(2x)/(7)+b`

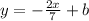
We can convert this to the standard form as indicated earlier;

`\begin{gathered} From\text{ the original equation; when} \\ x=4 \\ y=2(4)^2-4(4)^{(3)/(2)}-(8)/(4)-1 \\ y=32-4(8)-2-1 \\ y=32-32-2-1 \\ y=-3 \end{gathered}`

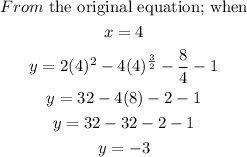
With the points

`(4,-3)`

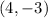
We now have, the equation;

`\begin{gathered} y=mx+b \\ -3=-(2(4))/(7)+b \\ -3=-(8)/(7)+b \end{gathered}`

We now collect like terms;

`\begin{gathered} b=(8)/(7)-3 \\ b=-(13)/(7) \end{gathered}`

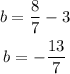
We now have the y-intercept as calculated above.

We can now write up our equation is the standard form as indicated from the beginning;

`\begin{gathered} ax+by+c=0 \\ (x,y)=(4,-3) \\ c=-(13)/(7) \end{gathered}`
`\begin{gathered} 4a+(-3)b+(-(13)/(7))=0 \\ 4a-3b-(13)/(7)=0 \end{gathered}`

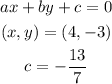
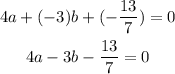
Note that A, B and C must be integers. Therefore, we multiply all through by 7;

ANSWER:

`28a-21b-13=0`