The original point has coordinates (11,-5)
The transformation applied to this point are Rx=0 * T(11,-5)
First, you have to do the translation T(11,-5), this means that you have to make a horizontal translation 11 units to the right, and a vertical translation 5 units down, following the rule:
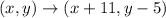
So, add 11 units to the x-coordinate and subtract 5 units to the y-coordinate of (11,-5)

Once you've made the translation, you have to reflect the point (22,-10) over the vertical line x=0, this vertical line is the y-axis. This means that you have to reflect the point over the y-axis.
To do this reflection you have to invert the sign of the x-coordinate of the point and leave the y-coordinate the same:
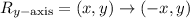
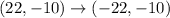
The coordinates of the point after the translation and reflection are (-22,-10), option 1