According to the figure we need to evaluate the sin(30°) and the cos(60°). Remember the trigonometric relations defined over the rectangle triangles as follows, suppose we have an angle called "alpha"

Now, according to the figure, we have that for the angle of 60 degrees:
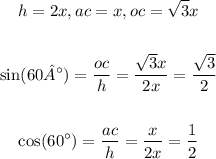
And for the angle of 30 degrees we get the following

So, your answer is: sin(30°)=1/2=cos(60°).