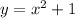The general equation for a quadratic equation is,
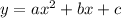
Substititute the values to obtain the equations for the coefficients.
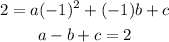
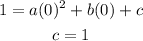
and
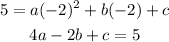
Substitute the value of c in the equation a-b+c=2 to obtain the equation for a and b.
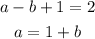
Substitute the value of a and c in the equation 4a-2b+c=5 to obtain the value of b.
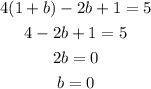
Substitute the value of b in the equation a=1+b to obtain the value of a.
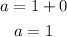
So quadratic equation for a=1, b=0 and c=1 is,