To obtain the surface area of a triangular prism, the formula to employ is:
![\begin{gathered} A_{triangular\text{ prism}}=2A_B+(a+b+c)h \\ \text{where A}_B=\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{where s=}(a+b+c)/(2) \\ a,b\text{ and c are sides of the triangular prism and h is the height} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ft5foybz340jb71m0m4jqdsllhci8zh70e.png)
From the image, a=18in, b=21in, c =15in and h=12in
We have to obtain the value of 's' first, from the equation:
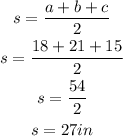
![\begin{gathered} \text{Then, we obtain the value of A}_B \\ A_B=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A_B=\sqrt[]{27(27-18)(27-21)(27-15)} \\ A_B=\sqrt[]{27(9)(6)(12)} \\ A_B=\sqrt[]{17496} \\ A_B=132.27in^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/t5v79kevd5cl50ysdk4asyfeaqhs9bvrtd.png)
The final step is to obtain the area of the triangular, having gotten the values needed to be inputted in the formula;
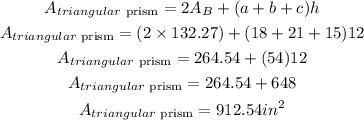
Hence, the surface area of the triangular prism is 912.54 square inches