Question

ow 3. Hto What is the surface area of this triangular prism? 15 in. 12 in. 7 21 in 18 in. A. 846 in. B. 909 in. C. 1,062 in. D. 1,224 in. 2

Answer 1

To obtain the surface area of a triangular prism, the formula to employ is:

`\begin{gathered} A_{triangular\text{ prism}}=2A_B+(a+b+c)h \\ \text{where A}_B=\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{where s=}(a+b+c)/(2) \\ a,b\text{ and c are sides of the triangular prism and h is the height} \end{gathered}`

From the image, a=18in, b=21in, c =15in and h=12in

We have to obtain the value of 's' first, from the equation:

`\begin{gathered} s=(a+b+c)/(2) \\ s=(18+21+15)/(2) \\ s=(54)/(2) \\ s=27in \end{gathered}`
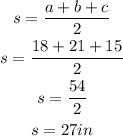
`\begin{gathered} \text{Then, we obtain the value of A}_B \\ A_B=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A_B=\sqrt[]{27(27-18)(27-21)(27-15)} \\ A_B=\sqrt[]{27(9)(6)(12)} \\ A_B=\sqrt[]{17496} \\ A_B=132.27in^2 \end{gathered}`

The final step is to obtain the area of the triangular, having gotten the values needed to be inputted in the formula;

`\begin{gathered} A_{triangular\text{ prism}}=2A_B+(a+b+c)h \\ A_{triangular\text{ prism}}=(2*132.27)+(18+21+15)12 \\ A_{triangular\text{ prism}}=264.54+(54)12 \\ A_{triangular\text{ prism}}=264.54+648 \\ A_{triangular\text{ prism}}=912.54in^2 \end{gathered}`

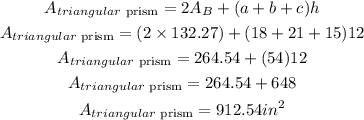
Hence, the surface area of the triangular prism is 912.54 square inches