We can see from the question that we have the following function:
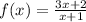
And we need to find the rate of change from x = 0 to x = 2.
1. To find the average rate of change, we need to remember the formula to find it:
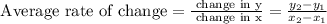
And we also have the average rate of change for a function, f(x) between x = a and x = b is given by:
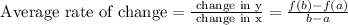
2. Then we have that the average rate of change between x = 0 and x = 2 is as follows:

3. However, we need to find the values for the function when f(2) and f(0). Then we have:

And we also have:

4. Finally, the average rate of change is given by:
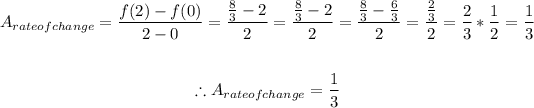
Therefore, in summary, we have that the average rate of change of the function:
