Answer:
a. v = 40 000 (3/ 5)^d
b. v = 40 000 (3/5)^(4/10)
c. 0.95
Step-by-step explanation:
The exponential growth is modelled by
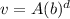
We know that points (0, 40 000) and (1, 24 000) lie on the curve. This means, the above equation must be satsifed for v = 40 000 and d = 0. Putting v = 40 000 and d = 0 into the above equation gives
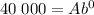
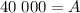
Therefore, we have
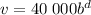
Similarly, from the second point (1, 24 000) we put v = 24 000 and d = 1 to get
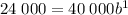
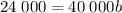
dividing both sides by 40 000 gives
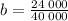
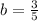
Hence, our equation that models the situation is

Part B.
Remember that the d in the equation we found in part A is decades. Since there are 10 years in a decade, we can write
t = 10d
or
d = t/10
Where t = number of years
Making the above substitution into our equation gives
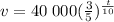
Therefore, the car's value at t = 4 is
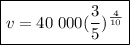
Part C:
The equation that gives the car's value after t years is
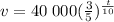
which using the exponent property that x^ab = (x^a)^b we can rewrite as
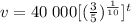
Since
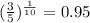
Therefore, our equation becomes
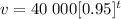
This tells us that the car's value is changing by a factor of 0.95 each year.