Question

4.

The value of a truck decreases exponentially since its purchase. The two points on the
graph shows the truck's initial
value and its value a decade afterward.
[6040,000)
a) Express the car's value, in dollars, as a function of time
d, in decades, since purchase.
(1 24,000)
b) Write an expression to represent the car's value 4 years
after purchase.
c) By what factor is the value of the car changing each year? Show your reasoning.

Answer 1

a. v = 40 000 (3/ 5)^d

b. v = 40 000 (3/5)^(4/10)

c. 0.95

Step-by-step explanation:

The exponential growth is modelled by

`v=A(b)^d`

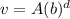
We know that points (0, 40 000) and (1, 24 000) lie on the curve. This means, the above equation must be satsifed for v = 40 000 and d = 0. Putting v = 40 000 and d = 0 into the above equation gives

`40\; 000=Ab^0`

`40\; 000=A`

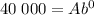
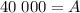
Therefore, we have

`v=40\; 000b^d`

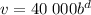
Similarly, from the second point (1, 24 000) we put v = 24 000 and d = 1 to get

`24\; 000=40\; 000b^1`
`24\; 000=40\; 000b^{}`

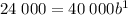
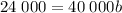
dividing both sides by 40 000 gives

`b=(24\; 000)/(40\; 000)`
`b=(3)/(5)`

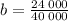
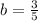
Hence, our equation that models the situation is

`\boxed{v=40\; 000((3)/(5))^d\text{.}}`

Part B.

Remember that the d in the equation we found in part A is decades. Since there are 10 years in a decade, we can write

t = 10d

or

d = t/10

Where t = number of years

Making the above substitution into our equation gives

`v=40\; 000((3)/(5))^{(t)/(10)}`

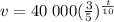
Therefore, the car's value at t = 4 is

`\boxed{v=40\; 000((3)/(5))^{(4)/(10)}}`

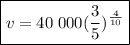
Part C:

The equation that gives the car's value after t years is

`v=40\; 000((3)/(5))^{(t)/(10)}`

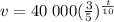
which using the exponent property that x^ab = (x^a)^b we can rewrite as

`v=40\; 000\lbrack((3)/(5))^{(1)/(10)}\rbrack^t`

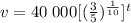
Since

`((3)/(5))^{(1)/(10)}=0.95`

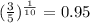
Therefore, our equation becomes

`v=40\; 000\lbrack0.95\rbrack^t`

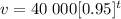
This tells us that the car's value is changing by a factor of 0.95 each year.