Find the value of x that makes A || B.AB5423142 3x10 and 23 = x + 30X=[? ]

Question

asked Jul 18, 2023 99.8k views

1 Answer

Neaumusic · Answer 1 · 2023-07-24T19:29:33+0000

∠2 and ∠3 are alternate interior angles. In order to A II B, the alternate interior angles must be equal.

Then,

$\begin{gathered} \angle2=\operatorname{\angle}3 \\ 3x-10=x+30 \end{gathered}$

To find x, subtract x from both sides of the equation:

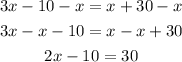
$\begin{gathered} 3x-10-x=x+30-x \\ 3x-x-10=x-x+30 \\ 2x-10=30 \end{gathered}$

Now, add 10 to both sides of the equation:

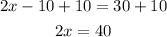
$\begin{gathered} 2x-10+10=30+10 \\ 2x=40 \end{gathered}$

Finally, divide both sides by 2:

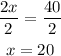
$\begin{gathered} (2x)/(2)=(40)/(2) \\ x=20 \end{gathered}$

Answer: x = 20.