Question

Find the value of x that makes A || B.AB5423142 3x10 and 23 = x + 30X=[? ]

Answer 1

∠2 and ∠3 are alternate interior angles. In order to A II B, the alternate interior angles must be equal.

Then,

To find x, subtract x from both sides of the equation:

`\begin{gathered} 3x-10-x=x+30-x \\ 3x-x-10=x-x+30 \\ 2x-10=30 \end{gathered}`

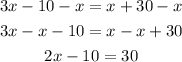
Now, add 10 to both sides of the equation:

`\begin{gathered} 2x-10+10=30+10 \\ 2x=40 \end{gathered}`

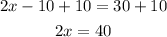
Finally, divide both sides by 2:

`\begin{gathered} (2x)/(2)=(40)/(2) \\ x=20 \end{gathered}`

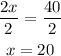
Answer: x = 20.