Question

If the number of bacteria in a colony doubles every 236 minutes and there is currently a population of 9,085 bacteria, what will the population be 708 minutes from now?

Answer 1

We could state an exponential model.

Number of bateria will be given by:

`N=N_0e^(kt)`

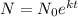
where k=growth constant and t=time in minutes.

We're given that N0 is the initial population, which is:

`N_0=9,085`

We also know that, when t=236 min, N=2(9,085) = 18,170:

`18,170=9,085e^(k(236))^{}`

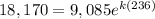
We're going to solve this equation to find the value of k:

`\begin{gathered} (18,170)/(9,085)=e^(236k) \\ 2=e^(236k) \\ \ln 2=\ln e^(236k) \\ \ln 2=236k \\ k=(\ln 2)/(236) \end{gathered}`

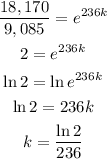
Then, our expression is:

`N=9,085e^{(\ln 2)/(236)t}`

To find the population of bacteria after 708 minutes, we replace t by 708:

`N=9085e^{(\ln2)/(236)(708)}=72680`

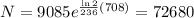
Therefore, the population of bacteria 708 minutes from now, is 72680.