We are given that a train is traveling at the following constant speed:
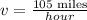
We are asked to determine the distance after 3 seconds. To do that, let's remember that speed is the ratio between distance and time, that is:
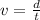
Where:
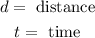
Since we want to determine the distance we will multiply both sides of the equation by "t":
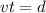
Now, we substitute the values:
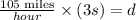
Since the velocity is given per unit of hour, we need to convert the 3 seconds into hours. We do that using the following conversion factor:
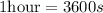
Now we multiply the time by the conversion factor:
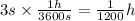
Now we substitute in the formula for the distance:
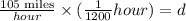
Solving the operations:
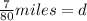
Now, we convert the miles into feet using the given conversion factor:
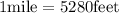
Now, we multiply by the conversion factor:
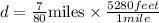
Solving the operations:
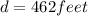
Therefore, the distance is 462 feet.