Question

The point P. = (x,1/3) lies on the unit circle shown below. What is the value of x insimplest form?

Answer 1

When a point (x,y) lies on a unit circle, the following equation holds true:

`x^2+y^2=1`

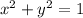
We are given

`y=(1)/(3)`

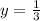
and need to find x.

Let's put it into the equation and figure out x. Shown below:

`\begin{gathered} x^2+y^2=1 \\ x^2+((1)/(3))^2=1 \\ x^2+(1)/(9)=1 \\ x^2=1-(1)/(9) \\ x^2=(8)/(9) \\ x=\sqrt[]{(8)/(9)} \\ x=\frac{\sqrt[]{8}}{\sqrt[]{9}} \\ x=\frac{\sqrt[]{8}}{3} \end{gathered}`

We can simplify the square root of 8 by using the radical property:

`\sqrt[]{a\cdot b}=\sqrt[]{a}\sqrt[]{b}`

Thus, square root of 8 becomes:

`\sqrt[]{8}=\sqrt[]{4\cdot2}=\sqrt[]{4}\sqrt[]{2}=2\sqrt[]{2}`

Thus, the simplest form of x is:

`x=\frac{2\sqrt[]{2}}{3}`