Question

The lenath of an instant message conversation is normally distributed with a mean of 5 minutes and a standard deviation of .7 minutes. What is the probability that a conversation lasts longer than 6 minutes?

Answer 1

To solve this problem we can use a z-table. First, we convert our score to a z-score using the following formula:

`z=(x-\mu)/(\sigma)`

where mu represents the mean and sigma represents the standard deviation.

Using this formula in our problem, we have:

`z=(6-5)/(0.7)=(10)/(7)\approx1.429`

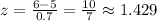
This z-score represents the position where the phone call is equal to 6 minutes. On a z-table, we're going to find the area between the mean and this z-score, since we want the probability that a conversation lasts longer than 6 minutes, we want the area above it. To calculate this area, we're going to subtract the value given on the z-table from 0.5.

The value on the z-table is:

Then, our probability is:

`P(x>6)=0.5-0.4236\approx0.077`

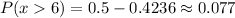
The answer is 0.077.