Question

The following equations are givenEquation #1 3x+z+y=8Equation #2 5y-x=-7Equation #3 3z+2x-2y=15Equation #4 4x+5y-2z=-3a. is it possible to solve for any of the variables using only Equation #1 and Equation #27 Explain your answer. If possible, solve for the variables using only equations #1 and #2b. is it possible to solve for any of the variables using only Equation #1, Equation #2, and Equation #37 Explain your answer if possible, solve for the variables using only equations #1, #2, and #3c. if you found solutions in part b, do these solutions also hold for Equation #4?

Answer 1

(a). For any number of equations to be solved simultaneously, the number of equations, must be same as number of variables.

Hence, Equation (1) & (2) can't be solved simultaneously, because, only two equations are given to solve for 3 variables.

(b) From the explanation above, it is obvious that, Equation (1), (2), and (3), can be solved simultaneously, because, we have 3 variables (x, y, z), with 3 equations to solve with.

Next we do is to solve Equation (1), (2), and (3) simultaneously using substitution method.

`\begin{bmatrix}3x+z+y=8\\ 5y-x=-7\\ 3z+2x-2y=15\end{bmatrix}`

From the Equation 2, make y the subject of formula

`\begin{gathered} 5y-x=-7 \\ 5y=-7+x \\ y=(-7+x)/(5) \end{gathered}`

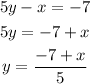
We substitute, for y in equation (1), and (3).

`\begin{bmatrix}3x+z+(-7+x)/(5)=8\\ 3z+2x-2\cdot (-7+x)/(5)=15\end{bmatrix}`

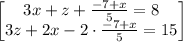
Simplifying,

`\begin{bmatrix}z+(-7+16x)/(5)=8\\ 3z+(14+8x)/(5)=15\end{bmatrix}`

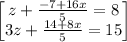
make z the subject of formula

`z=8-(-7+16x)/(5)`

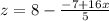
Substitute z in the second equation,

`\begin{gathered} \begin{bmatrix}3\left(8-(-7+16x)/(5)\right)+(14+8x)/(5)=15\end{bmatrix} \\ simplifying \\ \begin{bmatrix}-8x+31=15\end{bmatrix} \\ simplifying \\ -8x=15-31=-16 \\ x=(-16)/(8)=-2 \end{gathered}`

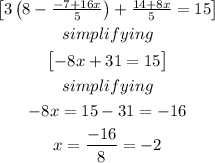
Now, we have the value of x, remaining y, and z, and we substitute the value of x = -2, in the equation above for z.

`\begin{gathered} z=8-(-7+16x)/(5) \\ z=8-(-7+16(2))/(5)=(-7+32)/(5) \\ z=(25)/(5)=5 \end{gathered}`
`\begin{gathered} y=(-7+x)/(5)=(-7+2)/(5)=(5)/(5)=1 \\ y=1 \end{gathered}`

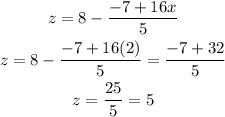
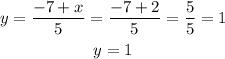
Hence, x = -2, y = 1, z = 5

(c)

Next, we proof for the values of x, y, and z in equation (4)

Substitute, x = -2, y = 1, z = 5 in equation (4)

`\begin{gathered} 4x+5y-2z=-3 \\ 4(-2)+5(1)-2(5)=-8+5-10=-13\\e-3 \\ \end{gathered}`

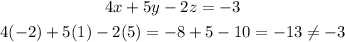
Hence, the solution doesn't hold for the equation (4).