Answer:
1077.19 ft
Step-by-step explanation:
Using the depression angle, we get that one of the angles of the formed triangle is also 18° because they are alternate interior angles, so we get:
Now, we can relate the distance x, the angle of 18°, and the height of the tower using the trigonometric function tangent, so:
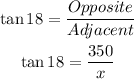
Now, solving for x, we get:
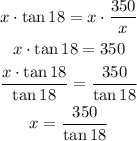
Using the calculator, we get that tan(18) = 0.325, so x is equal to:
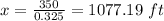
Therefore, the forest ranger is at 1077.19 ft from the fire.