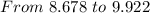Question

A recent study of 28 city residents showed that the mean of the time they had lived at their present address was 9.3 years. The standard deviation of the population was 2 years. Find the 90% confidence interval of the true mean? Assume that the variable is approximately normally distributed. Show all your stepsVery confused in this exercise I’m self teaching myself

Answer 1

Given that:

- The sample size is 28 city residents:

`n=28`

- The mean of the time (in years) they had lived at their present address was:

`\mu=9.3`

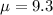
- The standard deviation (in years) of the population was:

`\sigma=2`

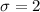
Then, you need to use the following formula for calculating the Confidence Interval given the Mean:

`C.I.=\mu\pm z(\sigma)/(√(n))`

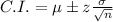
Where μ is the sample mean, σ is the standard deviation, "z" is the z-score, and "n" is the sample size.

By definition, the z-score for a 90% confidence interval is:

`z=1.645`

Therefore, you can substitute values into the formula and evaluate:

`C.I.=9.3\pm(1.645)((2)/(√(28)))`

You get that the lowest value is:

`9.3-(1.645)((2)/(√(28)))\approx8.678`

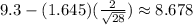
And the highest value is:

`9.3+(1.645)((2)/(√(28)))\approx9.922`

Hence, the answer is:

`From\text{ }8.678\text{ }to\text{ }9.922`