Question

You need to ride an average of at least 35 miles per day for five consecutive days toqualify for a cross-country biking expedition. The distances (in miles) of your rides in thefirst four days are 45, 33, 27, and 26. What distances on the fifth day will allow you toqualify for the competition?

Answer 1

We are to maintain a constant mean distance of ( d-avg ) to qualify for the cross-country biking expedition.

The qualification for the expedition is to rirde an average distance of:

`d_(avg)\text{ }\ge\text{ 35 miles each for 5 consecutive day }`

We are already on target for 4 days. For which we covered a distance ( d ) for each day:

`\begin{gathered} \text{\textcolor{#FF7968}{Day 1:}}\text{ 45 miles} \\ \text{\textcolor{#FF7968}{Day 2:}}\text{ 33 miles} \\ \text{\textcolor{#FF7968}{Day 3:}}\text{ 27 miles} \\ \text{\textcolor{#FF7968}{Day 4: }}\text{26 miles} \end{gathered}`

We are to project how much distance we must cover atleast on the fifth day ( Day 5 ) so that we can qualify for the expedition. The only condition for qualifying is given in terms of mean distance traveled over 5 days.

The mean value of the distance travelled over ( N ) days is expressed mathematically as follows:

`d_(avg)\text{ =}\sum ^N_(i\mathop=1)(d_i)/(N)`

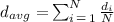
Where,

`\begin{gathered} d_i\colon Dis\tan ce\text{ travelled on ith day} \\ N\colon\text{ The total number of days in consideration} \end{gathered}`

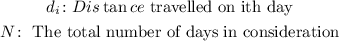
We have the data available for the distance travelled for each day ( di ) and the total number of days in consideration ( N = 5 days ). We will go ahead and used the standard mean formula:

`d_(avg)\text{ = }(d_1+d_2+d_3+d_4+d_5)/(5)`

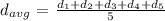
Then we will apply the qualifying condtion to cover atleast 35 miles for each day for the course of 5 days.

`(45+33+27+26+d_5)/(5)\ge\text{ 35}`

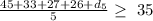
Then we will solve the above inequality for Day 5 - (d5) as follows:

`\begin{gathered} d_5+131\ge\text{ 35}\cdot5 \\ d_5\ge\text{ 175 - 131} \\ \textcolor{#FF7968}{d_5\ge}\text{\textcolor{#FF7968}{ 44 miles}} \end{gathered}`

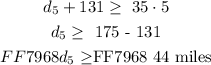
The result of the above manipulation shows that we must cover a distance of 44 miles on the 5th day so we can qualify for the expedition! So the range of distances that we should cover atleast to qualify is:

`\textcolor{#FF7968}{d_5\ge}\text{\textcolor{#FF7968}{ 44 miles}}`

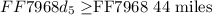
All covered distances greater than or equal to 44 miles will get us qualified for the competition!