Question

Rhombus ABCD with vertices A(1,0), B(6,-2), C(8,-7), and D(3,-5); 90° counterclockwise rotation about the origin

Answer 1

Given data:

The given coordinates of Rhombus are A(1,0), B(6,-2), C(8,-7), and D(3,-5).

The coordinate of a point after 90 degrees counterclockwise rotation is,

`(x,\text{ y)}\rightarrow(-y,x)`

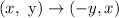
The final coordinate of Rhombus are,

`\begin{gathered} A(1,0)=A^(\prime)(0,\text{ 1)} \\ B(6,\text{ -2)=B'(2, 6)} \\ C(8,\text{ -7)=C'(7},\text{ 8)} \\ D(3,\text{ -5)=D'(5, 3)} \end{gathered}`

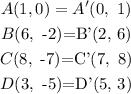
Thus, the final coordinate of Rhombus are A'(0,1), B'(2, 6), C'(7, 8) and D'(5, 3).