Given data:
The given coordinates of Rhombus are A(1,0), B(6,-2), C(8,-7), and D(3,-5).
The coordinate of a point after 90 degrees counterclockwise rotation is,
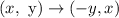
The final coordinate of Rhombus are,
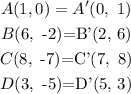
Thus, the final coordinate of Rhombus are A'(0,1), B'(2, 6), C'(7, 8) and D'(5, 3).