Question

The safe load, L, of a wooden beam of width w, height h and length l, supported at both ends, varies directly as the product of the width and the square of the height and inversely as the length. A wooden beam 5 inches wide, 7 inches high and 144 inches long can hold a load of 8740 pounds. What load would a beam 6 inches wide, 9 inches high, and 216 inches long of the same material, support? Round your answer to the nearest integer if necessary.

Answer 1

Since the load L varies directly with the product of width and square of the height h, and inveresly as the length l, so

`\begin{gathered} L=k((wh^2)/(l)) \\ OR \\ (L_1)/(L_2)=(w_1)/(w_2)*(h^2_1)/(h^2_2)*(l_2)/(l_1) \end{gathered}`

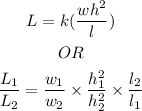
We will use the second rule

Since L is 8740 pounds when w is 5 in., h is 7 in. and l is 144 in.

`\begin{gathered} L_1=8740 \\ w_1=5 \\ h_1=7 \\ l_1=144 \end{gathered}`

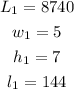
We need to find L when w is 6 in., h is 9 in. and l is 216 in.

`\begin{gathered} L_2=? \\ w_2=6 \\ h_2=9 \\ l_2=216 \end{gathered}`

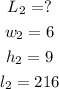
Let us substitute them in the second rule

`\begin{gathered} (8740)/(L_2)=(5)/(6)*(7^2)/(9^2)*(216)/(144) \\ (8740)/(L_2)=(5)/(6)*(49)/(81)*(216)/(144) \\ (8740)/(L_2)=(245)/(324) \end{gathered}`

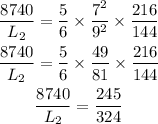
By using cross multiplication

`\begin{gathered} 245* L_2=8740*324 \\ 245L_2=2831760 \end{gathered}`

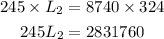
Divide both sides by 245

`\begin{gathered} (245L_2)/(245)=(2831760)/(245) \\ L_2=11558.20408 \end{gathered}`

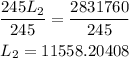
Round it to the nearest integer

`L_2=11558\text{ pounds}`

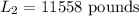
The load is 11558 pounds