Since the load L varies directly with the product of width and square of the height h, and inveresly as the length l, so
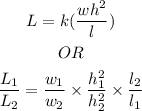
We will use the second rule
Since L is 8740 pounds when w is 5 in., h is 7 in. and l is 144 in.
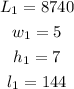
We need to find L when w is 6 in., h is 9 in. and l is 216 in.
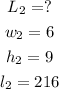
Let us substitute them in the second rule
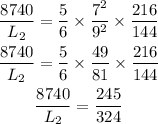
By using cross multiplication
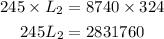
Divide both sides by 245
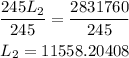
Round it to the nearest integer
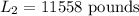
The load is 11558 pounds