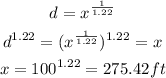Question

The formula for calculating the distance, d, in miles that one can see to the horizon on a clear day is approximated by d=1.22radical x, where x is the elevation in feet of a person's eyes. a. approximately how far, to the nearest mile, can a person whose eyes are 600 feet above sea-level see? b. approximately how high, to the nearest foot, would a person's eyes need to be to see 100 miles?

Answer 1

The expression to calculate the distance a person can see is below, where x is the height in feet of a person's eyes above see-level:

`d=\sqrt[1.22]{x}\lbrack mi\rbrack`

a) A person who is 600 feet height will see:

`d=\sqrt[1.22]{600}=189.30mi`

b) In order to get the height a person needs to be so that he/she could see 100 miles long, we solve the equation for x:

`\begin{gathered} d=x^{(1)/(1.22)} \\ d^(1.22)=(x^{(1)/(1.22)})^(1.22)=x \\ x=100^(1.22)=275.42ft \end{gathered}`