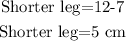Question

The hypotenuse of a right triangle is 1 centimeter longer than the longer leg. The shorter leg is 7 centimeters shorter than the longer leg. Find the length of the shorter leg of the triangle.

Answer 1

`\text{Shorter leg= 5cm}`

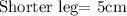
Explanation:

As a first step to go into this problem, we need to make a diagram:

Let x be the measure of the longer leg.

Now, understanding this we can apply the Pythagorean theorem to find x, it is represented by the following equation:

`\begin{gathered} a^2+b^2=c^2 \\ \text{where,} \\ a=\text{longer leg} \\ b=\text{shorter leg} \\ c=\text{hypotenuse } \end{gathered}`

Substituting a,b, and c by the expressions corresponding to its sides:

`\begin{gathered} x^2+(x-7)^2=(x-1)^2 \\ \end{gathered}`

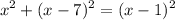
apply square binomials to expand and gather like terms, we get:

`\begin{gathered} x^2+x^2-14x+49=x^2-2x+1 \\ 2x^2-x^2-14x+2x+49-1=0 \\ x^2-12x+48=0 \end{gathered}`

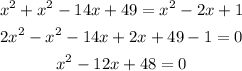
Now, factor the quadratic equation into the form (x+?)(x+?):

`\begin{gathered} (x-4)(x-12)=0 \\ x_1=4 \\ x_2=12 \end{gathered}`

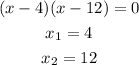
This means, the longer leg could be 4 or 12, but if we subtract 7 to 4, we get a negative measure for the shorter leg, that makes no sense.

Therefore, the long leg is 12 cm.

Hence, if the shorter leg is 7 centimeters shorter than the longer leg:

`\begin{gathered} \text{Shorter leg=12-7} \\ \text{Shorter leg=}5\text{ cm} \end{gathered}`