Given,
The mass of puck A, m₁=0.0380 kg
The mass of puck B, m₂=0.0760 kg
The velocity of puck A before the collision, u=+6.29 m/s
The angle made by puck A with the x-axis, θ₁=65°
The angle made by puck B, θ₂=-37°
The momentum is conserved in both directions simultaneously and independently. That is, the sum x-components of the momentum before the collision and after the collision are equal. The same goes for the y-axis.
Considering the x-direction,
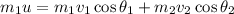
Where v₁ is the velocity of puck A and v₂ is the velocity of puck B after the collision.
On substituting the known values,
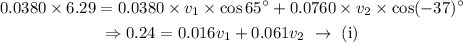
Considering the y-direction,
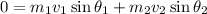
On substituting the known values,
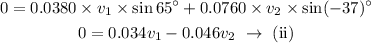
On solving equations (i) and (ii),
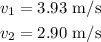
Thus the speed of pluck A is 3.93 m/s and the speed of pluck B is 2.90 m/s