Question

2 pucks on an air-hockey table. Puck A has a mass of 0.0380 kg and is moving along the x axis with a velocity of + 6.29 m/s. It takes a collision with puck B, which has a mass of 0.0760 kg and is initially at rest. The collision is not head-on. After the collision, the two pucks fly apart with the angle shown in the drawing, pluck A at an angle of 65 degrees to the x axis and pluc B at an angle of -37 degrees to the x axis. Find the speed of pluck A and pluck B.

Answer 1

Given,

The mass of puck A, m₁=0.0380 kg

The mass of puck B, m₂=0.0760 kg

The velocity of puck A before the collision, u=+6.29 m/s

The angle made by puck A with the x-axis, θ₁=65°

The angle made by puck B, θ₂=-37°

The momentum is conserved in both directions simultaneously and independently. That is, the sum x-components of the momentum before the collision and after the collision are equal. The same goes for the y-axis.

Considering the x-direction,

`m_1u=m_1v_1\cos \theta_1+m_2v_2\cos \theta_2`

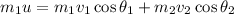
Where v₁ is the velocity of puck A and v₂ is the velocity of puck B after the collision.

On substituting the known values,

`\begin{gathered} 0.0380*6.29=0.0380* v_1*\cos 65^(\circ)+0.0760* v_2*\cos (-37)^(\circ) \\ \Rightarrow0.24=0.016v_1+0.061v_2\text{ }\rightarrow\text{ (i)} \end{gathered}`

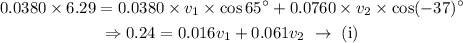
Considering the y-direction,

`0=m_1v_1\sin \theta_1+m_2v_2\sin \theta_2`

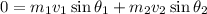
On substituting the known values,

`\begin{gathered} 0=0.0380* v_1*\sin 65^(\circ)+0.0760* v_2*\sin (-37)^(\circ) \\ 0=0.034v_1-0.046v_2\text{ }\rightarrow\text{ (ii)} \end{gathered}`

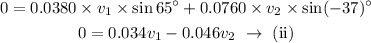
On solving equations (i) and (ii),

`\begin{gathered} v_1=3.93\text{ m/s} \\ v_2=2.90\text{ m/s} \end{gathered}`

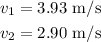
Thus the speed of pluck A is 3.93 m/s and the speed of pluck B is 2.90 m/s