We are given that Gloria jumps from a bridge using a bungee cord. The quadratic expression that models an object falling freely is the following:
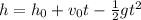
Where:

A representation of the problem is the following:
If we assume that the initial velocity is zero, we get the following values:
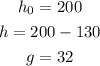
The height is equivalent to the total height of the bridge minus the longitude of the cord. The value for "g" is a constant equivalent to 32 feet per second.
Replacing we get:
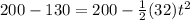
Now we solve for "t", first by subtracting 200 to both sides:
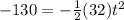
Solving the operation:
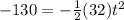
Multiplying both sides by -2:
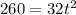
Dividing both sides by 32:
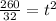
Taking square root on both sides of the equation:
![\sqrt[]{(260)/(32)}=√(t^2)](https://img.qammunity.org/2023/formulas/mathematics/college/pb6zcjviyoyus6fienxmss6q7222dwng9z.png)
Solving the operations:
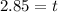
Therefore, the cord starts stretching at 2.85 seconds.