Question

Gloria, an experienced bungee jumper, leaps from a tall bridge and falls toward the river below. The bridge is 200 feet above the water and Gloria's bungee cord is 130 feet long unstretched. When will Gloria's cord begin to stretch? Round your answer to two decimal places.

Answer 1

We are given that Gloria jumps from a bridge using a bungee cord. The quadratic expression that models an object falling freely is the following:

`h=h_0+v_0t-(1)/(2)gt^2`

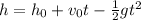
Where:

`\begin{gathered} h_0=\text{initial height} \\ v_0=\text{initial velocity} \\ g=\text{acceleration of gravity} \\ t\text{ = time} \end{gathered}`

A representation of the problem is the following:

If we assume that the initial velocity is zero, we get the following values:

`\begin{gathered} h_0=200 \\ h=200-130 \\ g=32 \\ \end{gathered}`

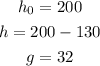
The height is equivalent to the total height of the bridge minus the longitude of the cord. The value for "g" is a constant equivalent to 32 feet per second.

Replacing we get:

`200-130=200-(1)/(2)(32)t^2`

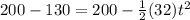
Now we solve for "t", first by subtracting 200 to both sides:

`-130=-(1)/(2)(32)t^2`

Solving the operation:

`-130=-(1)/(2)(32)t^2`

Multiplying both sides by -2:

`260=32t^2`

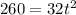
Dividing both sides by 32:

`(260)/(32)=t^2`

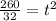
Taking square root on both sides of the equation:

`\sqrt[]{(260)/(32)}=√(t^2)`

Solving the operations:

`2.85=t`

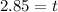
Therefore, the cord starts stretching at 2.85 seconds.