Question

Is the point (-2,11) on the circle with radius 5 and center (2,13)?

Answer 1

From the question;

we are to determine if the point (-2, 11) is on the circle with radius 5 and center (2, 13)

The equation of a circle with a radius r and center (a, b) is given as

`(x-a)^2+(y-b)^2=r^2`

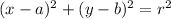
Hence, the equation of the circle with radius 5 and center (2, 13)

`\begin{gathered} (x-2)^2+(y-13)^2=5^2 \\ (x-2)^2+(y-13)^2\text{ = 25} \end{gathered}`

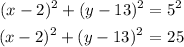
Considering the point (-2, 11), we need to substitute the values for x and y

therefore, x = -2, y = 11

`\begin{gathered} (-2-2)^2+(11-13)^2\text{ }\\e\text{ 25} \\ (-4)^2+(-2)^2\text{ }\\e\text{ 25} \\ 16\text{ + 4 }\\e\text{ 25} \\ 20\text{ }\\e\text{ 25} \end{gathered}`

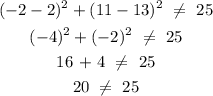
Since LHS is not equal to RHS then the point (-2, 11) is not on the circle.