Question

A chemist wishes to mix a solution that is 6% acid. She has on hand 14 liters of a 4% acid solution and wishes to add some 10% acid solution to obtain the desired 6% acid solution. How much 10% acid solution should she add?

Answer 1

she should add 7 liters of 10% acid solution

Step-by-step explanation

Step 1

set the equation:

a) let X represents the amount os solution that is 4% acid

let Y represents the amount os solution that is 10% acid

so

I)

`\begin{gathered} (4)/(100)X+(10)/(100)Y=(6)/(100)(x+y) \\ \end{gathered}`

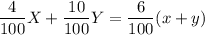
if he has 14 liters of 4% acid solution

`x=14`

`\begin{gathered} (4)/(100)X+(10)/(100)Y=(6)/(100)(X+Y) \\ (4)/(100)*14+(10)/(100)Y=(6)/(100)(X+Y) \\ 0.56+0.1Y=0.06(14+Y) \\ 0.56+0.1Y=0.84+0.06Y \\ \end{gathered}`

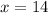
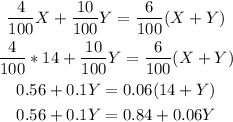
Step 2

solve the equation :

`\begin{gathered} 0.56+0.1Y=0.84+0.06Y \\ subtract\text{ 0.06Y in both sides} \\ 0.56+0.1Y-0.06Y=0.84+0.06Y-0.06Y \\ 0.56+0.04Y=0.84 \\ subtract\text{ 0.56 in both sides} \\ 0.56+0.04Y-0.56=0.84-0.56 \\ 0.04Y=0.28 \\ divide\text{ both sides by 0.04} \\ (0.04Y)/(0.04)=(0.28)/(0.04) \\ Y=7 \end{gathered}`

therefore,

she should add 7 liters of 10% acid solution

I hope this helps you