she should add 7 liters of 10% acid solution
Step-by-step explanation
Step 1
set the equation:
a) let X represents the amount os solution that is 4% acid
let Y represents the amount os solution that is 10% acid
so
I)
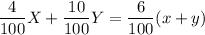
if he has 14 liters of 4% acid solution
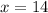
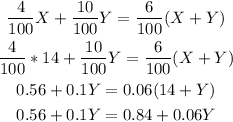
Step 2
solve the equation :
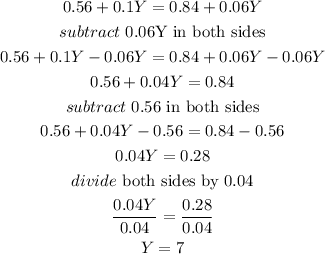
therefore,
she should add 7 liters of 10% acid solution
I hope this helps you