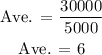Question

In the cost function below, C(x) is the cost of producing x items. Find the average cost per item when the required number of items is produced. C(x) = 4.1% +9,500 a. 200 items b. 2000 itemsC. 5000 items What is the average cost per item when 200, 2000, and 5000 items ?

Answer 1

Since the function of the cost is

`C(x)=4.1x+9500`

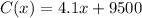
Where x is the number of the items

a) There were 200 items

x = 200

`\begin{gathered} C(x)=4.1(200)+9500 \\ C(x)=820+9500 \\ C(x)=10320 \end{gathered}`

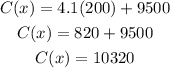
To find the average cost per item, find

`\begin{gathered} \text{Ave. =}(C(x))/(x) \\ \text{Ave. = }(10320)/(200) \\ \text{Ave. =51.6} \end{gathered}`

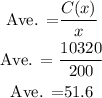
b) There were 2000 items

`x=2000`

`\begin{gathered} C(2000)=4.1*2000+9500 \\ C(2000)=17700 \end{gathered}`

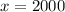
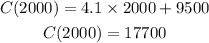
Find the average as the same above

`\begin{gathered} \text{Ave. = }(17700)/(2000) \\ \text{Ave. = 8.85} \end{gathered}`

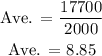
c) There were 5000 items

`x=5000`
`\begin{gathered} C(5000)=4.1(5000)+9500 \\ C(5000)=30000 \end{gathered}`

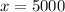
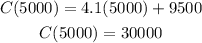
Divide it by 5000 to find the average

`\begin{gathered} \text{Ave. = }(30000)/(5000) \\ \text{Ave. = 6} \end{gathered}`