Since the function of the cost is

Where x is the number of the items
a) There were 200 items
x = 200

To find the average cost per item, find
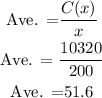
b) There were 2000 items
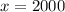

Find the average as the same above
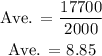
c) There were 5000 items


Divide it by 5000 to find the average
