We will reason to find the values of angles 1 through 6. To do so, we will use a key fact of triangles which is:
the sum of the angles of a triangle is 180°.
So, we will start by finding the value of angle 1. Note that angle 1 is in the triangle XYZ, whose other angles are 58° and 65°. Then, we have the following equation
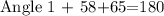
Since 58+65 = 123 then we have

By subtracting 123 on both sides, we get that

So angle 1 measures 57°.
We can see that angles 1 and 2 are supplementary. That is, their measures add up to 180°. So, we have the following equation
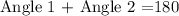
Since angle 1 = 77° we have that
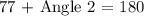
which implies that angle 2 measures 123°. Using the same principle we can find the value of angle 5, since we have
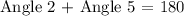
since angle 2 measures 123, we have that
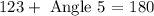
which implies that angle 5 measures 57°. Now, we see that angle 6 is in triangle VXW, so we can find the value of angle 6 as follows
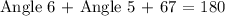
Then, since angle 5 measures 57° we have
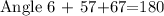
Since 57+67=124. Then , we have
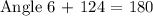
Subtracting 124 on both sides, we get
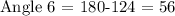
Now, we are missing to find the values of angles 3 and 4. To do so, first notice that

since these are the angles of triangle WXZ. We already know the measure of the angle 2 (123), so we have
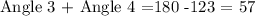
Unfortunately, the question doesn't give any more details on the triangles, so there are multiple solutions of values of angles 3 and 4 such that the equation holds