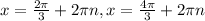Answer:
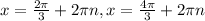
Explanation:
Given the equation:
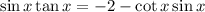
Add 2+cot(x)sin(x) to both sides of the equation.

Next, express in terms of sin and cos:
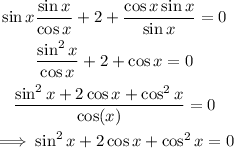
Apply the Pythagorean Identity: cos²x+sinx=1
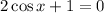
Subtract 1 from both sides:
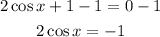
Divide both sides by 2:
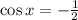
Take the arccos in the interval (-∞, ):
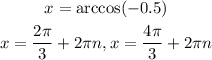
The values of x in the given interval are: