We are asked to determine the equation of a line with a slope 1/3. The general form of a line equation is:

Where "m" is the slope and "b" the y-intercept.
Now, we substitute the value of the slope:
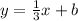
Now, to determine the value of "b" we will use the fact that the line passes through the point (x, y) = (
6, 8). Now, we plug in these values in the equation:
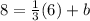
Solving the product on the right side we get:
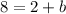
Now, we subtract 2 from both sides:
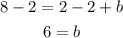
Now, we substitute the value in the equation of the line:
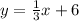
And thus we get the equation of the line.