Let us call x the number of $25 seats and y $40 seats, then we know that there are in total 5000 seats in a theatre; therefore, we have the equation
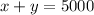
Also, after selling this many tickets the total revenue should be $149, 000; therefore, we get the equation
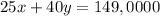
Hence, we have a system of equations with two equations and two unknowns.
We solve this system by substitution.
First, we solve for x in the first equation to get
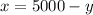
we then put this into the second equation to get
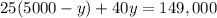
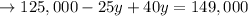
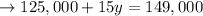
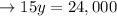
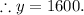
Now that we have y, we now solve for x to get:
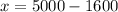
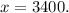
Hence x = 3400 and y = 1600 and the correct statements are as follows.
The number of tickets for sale at $25 should be 3400.
The number of tickets for sale at $40 should be 1600.