Question

A 5000-seat theater has tickets for sale at $25 and $40. How many tickets should be sold at each price for a sellout performance to generate a total revenue of $149,000? The number of tickets for sale at $25 should be ____ The number of tickets for sale at $40 should be ____

Answer 1

Let us call x the number of $25 seats and y $40 seats, then we know that there are in total 5000 seats in a theatre; therefore, we have the equation

`x+y=5000`

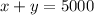
Also, after selling this many tickets the total revenue should be $149, 000; therefore, we get the equation

`25x+40y=149,0000`

Hence, we have a system of equations with two equations and two unknowns.

We solve this system by substitution.

First, we solve for x in the first equation to get

`x=5000-y`

we then put this into the second equation to get

`25(5000-y)+40y=149,000`
`\rightarrow125,000-25y+40y=149,000`
`\rightarrow125,000+15y=149,000`
`\rightarrow15y=24,000`
`\therefore y=1600.`

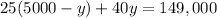
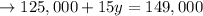
Now that we have y, we now solve for x to get:

`x=5000-1600`
`x=3400.`

Hence x = 3400 and y = 1600 and the correct statements are as follows.

The number of tickets for sale at $25 should be 3400.

The number of tickets for sale at $40 should be 1600. ​