Answer:
8 years
Explanation:
For a compound interest loan compounded annually, the amount due after t years is calculated using the formula:
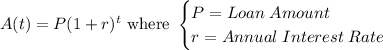
We want to find when the amount due will reach $64,000 or more.
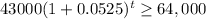
The equation is solved for t:
![\begin{gathered} \text{ Divide both sides by }43000 \\ (43,000(1+0.0525)^t)/(43000)\geqslant(64,000)/(43000) \\ (1.0525)^t\geq(64)/(43) \\ \text{Take the log of both sides:} \\ \log(1.0525)^t\geqslant\log((64)/(43)) \\ \text{By the power law of logarithm:} \\ \implies t\operatorname{\log}(1.0525)\geq\operatorname{\log}((64)/(43)) \\ \text{ Divide both sides by }\operatorname{\log}(1.0525) \\ t\geq\frac{\operatorname{\log}((64)/(43))}{\operatorname{\log}(1.0525)} \\ t\geq7.77 \end{gathered}]()
The number of years when the amount due will reach $64,000 or more is 8 years.