In order to find the value of a composition of functions at x = a, (f º g)(a), we first find the value of g(a), then find the value of f(x) at x = g(a).
(f º g)(a) = f(g(a))
In this problem, the values of f(x) and g(x) are shown in the table, for integer values of x from 0 to 9.
So, we have:
1. (f º g)(8) = f(g(8))
From the table, we see that
g(8) = 4 (value of g(x) in the line corresponding to x = 8)
Then:
f(g(8)) = f(4) = 4 (value of f(x) in the line corresponding to x = 4)
Thus:
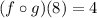
2. g(f(3))
f(3) = 8
g(8) = 4
Thus:
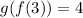
3. f(f(1))
f(1) = 6
f(6) = 2
Thus:

4. (g º g)(6) = g(g(6))
g(6) = 7
g(7) = 3
Thus:
