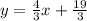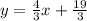
Step-by-step explanation
Given:
Point ( - 4, 1)
⇒x = -4 and y = 1
Perpendicular equation
3/4 x + y = -5/4
We need to re-write the above equation in the form y = mx + b
y = -3/4 x -5/4
Compare the above with y=mx + b where m is the slope and b is the intercept.
slope(m) = -3/4
Slope of vertical lines are inverse of one another.
This implies that the slpe of our new equation is:
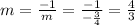
Next, is to find the intercept of the new equation.
We can find this by substituting m = 4/3 , x = -4 and y = 1 into y=mx + b and then solve for b.
That is;

We can proceed to form the new equation by simply substituting the values of m and b into y=mx + b
Hence, the equation is: