Question

Use the formula t= ln2 over k that gives the time for a population, with growth rate k, to double, to answer the following questions. The growth model A=6e^0.001t describes the population, A, of a country in millions, t years after 2003. A. What is the country's growth rate? B. (After answering A I will assistance for question B following question A)

Answer 1

A. k = 0.001

B. 693 years

Step-by-step explanation:

An exponential function has the following form:

`y=a\cdot e^(kt)`

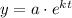
Where a is the initial value and k is the growth or decay rate.

So, if the equation is:

`A=6e^(0.001t)`

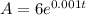
Therefore, the growth rate is 0.001.

Now, to know how long will it take the country to double its population, we can use the equation:

`t=(\ln 2)/(k)`

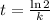
Where k is the growth rate. So, replacing k by 0.001, we get:

`\begin{gathered} t=(\ln 2)/(0.001) \\ t=693.14\approx693\text{ years} \end{gathered}`

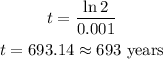
Therefore, the country will double its population 693 years after 2003