Question

Find the angle between the vectors u = 5i – 2j and v = 2i + 3j.

Answer 1

STEP - BY - STEP EXPLANATION

What to find?

The angle between the given vectors.

Given:

u = 5i – 2j and v = 2i + 3j.

To solve the given problem, we will follow the steps below:

Step 1

Write the formula that can be use to solve the above.

`cos\theta=\frac{\vec{a}\vec{.b}}\vec\vecb`

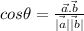
Step 2

Determine;

→ →

a. b

`\begin{gathered} \vec{a}\vec{.b}=(5)(2)+(-2)(3) \\ \\ =10-6 \\ \\ =4 \end{gathered}`

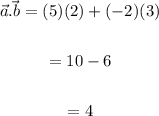
Step 3

Determine;

→ →

|a| and | b|

`\begin{gathered} \vec=√(5^2+(-2)^2) \\ \\ =√(25+4) \end{gathered}`
`=√(29)`

`\begin{gathered} \vec=√(2^2+3^2) \\ \\ =√(4+9) \\ \\ =√(13) \end{gathered}`

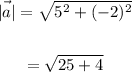
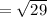
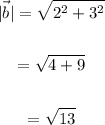
Step 4

Substitute the values into the formula.

`\begin{gathered} cos\theta=(4)/(√(29)*√(13)) \\ \\ =(4)/(√(377)) \end{gathered}`

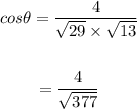
Step 5

Take the arc cos of both-side.

`\theta=cos^(-1)(0.20601)`
`\theta=78.1\degree`

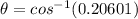
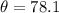
ANSWER

θ = 78. 1°